华中农业大学“瑞恒科技杯”
B题:货运公司的运输问题
某地区有8个公司(如图一编号①至⑧),某天某货运公司要派车将各公司所需的三种原材料A,B,C从某港口(编号⑨)分别运往各个公司。路线是唯一的双向道路(如图一)。货运公司现有一种载重 6吨的运输车,派车有固定成本20元/辆,从港口出车有固定成本为10元/车次(车辆每出动一次为一车次)。每辆车平均需要用15分钟的时间装车,到每个公司卸车时间平均为10分钟,运输车平均速度为60公里/小时(不考虑塞车现象),每日工作不超过8小时。运输车载重运费1.8元/吨公里,运输车空载费用0.4元/公里。一个单位的原材料A,B,C分别毛重4吨、3吨、1吨,原材料不能拆分,为了安全,大小件同车时必须小件在上,大件在下。卸货时必须先卸小件,而且不允许卸下来的材料再装上车,另外必须要满足各公司当天的需求量(见图二)。
问题:
1.货运公司派出运输车6辆,每辆车从港口出发(不定方向)后运输途中不允许掉头,应如何调度(每辆车的运载方案,运输成本)使得运费最小。
2. 每辆车在运输途中可随时掉头,若要使得成本最小,货运公司怎么安排车辆数?应如何调度?
3.选做
- (1)如果有载重量为4吨、6吨、8吨三种运输车,载重运费都是1.8元/吨公里,空载费用分别为0.2,0.4,0.7元/公里,其他费用一样,又如何安排车辆数和调度方案?
- (2)当各个公司间都有或者部分有道路直接相通时,分析运输调度的难度所在,给出你的解决问题的想法(可结合实际情况深入分析)。
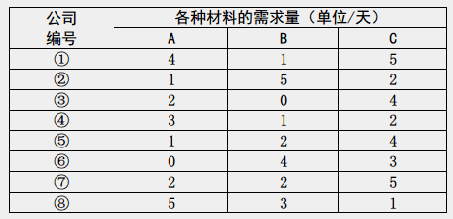
(图 一)唯一的运输路线图和里程数
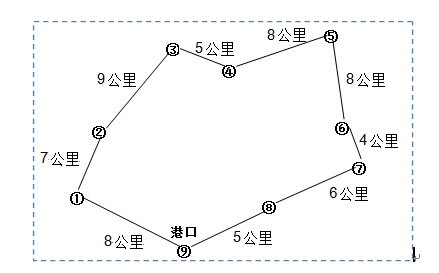
图 二)各个公司对每种材料的需求量(单位/天)
【摘要】本文深入研究了具有供求平衡、有序卸货特点的运输问题,建立最优化模型求解最小运费,采用启发式算法安排每辆车的运载方案。
在问题一的假设下,可以得出每次出车行程均相同的规律,显然存在贪婪因子(每次行车费用=运载费用+空载费用)。采用贪婪算法,在卸货顺序约束下对每次出车求局部最小费用且尽可能满载,最后得出全局解。通过启发式算法配车得到6辆车分别工作7.2511、7.0835、7.4187、6.1696、5.8344、5.8344(小时),总费用4771.2元,总运次27次(具体运载方案见5.1.3)。
在问题二的假设下,由于题中路程唯一,车速不变,可以得出如下定理:
一、车辆载重行程是各公司到港口最短路,且载重费用固定不变(5.2.1证明);
二、车辆当且仅当运完最后一件货才调头(5.2.1证明);
推论:运载里程与空载里程相同,且每次出车均不绕圈工作。
以所有定理为基础,加入卸货顺序约束,车容量约束,公司需求约束,以每次运输量![]() 为决策变量,最小总费用为目标,建立混合动态规划模型,使用LINGO软件编程求解最小运费及运次方案,通过启发式算法配车得到4辆车分别工作6.917、7.3838、5.7839、6.5338(小时),总费用4485.6元,总运次29次(具体运载方案见5.2.5)。
为决策变量,最小总费用为目标,建立混合动态规划模型,使用LINGO软件编程求解最小运费及运次方案,通过启发式算法配车得到4辆车分别工作6.917、7.3838、5.7839、6.5338(小时),总费用4485.6元,总运次29次(具体运载方案见5.2.5)。
问题三讨论存在多种容量货车时的运载方案,易证定理一、二及推论成立,在问题二模型基础上,引入0-1变量控制每次出车类型、车容量、空载费用,同样以每次运输量![]() 为决策变量,最小总费用为目标,建立混合动态规划模型,对求解结果(最小运费、运次方案,见5.3.2)按启发式算法配车,需要一辆6吨位车,工作7.4171(小时),运送5次;两辆8吨位车,工作时间分别为7.3005、7.135(小时),共运送16次(具体运载方案见5.3.4)。
为决策变量,最小总费用为目标,建立混合动态规划模型,对求解结果(最小运费、运次方案,见5.3.2)按启发式算法配车,需要一辆6吨位车,工作7.4171(小时),运送5次;两辆8吨位车,工作时间分别为7.3005、7.135(小时),共运送16次(具体运载方案见5.3.4)。
通过问题3结果分析,存在定理三:当空载运输路程大于![]() 公里的条件下才有可能存在4吨位车的使用。本题的空载运输路程都小于
公里的条件下才有可能存在4吨位车的使用。本题的空载运输路程都小于![]() 公里,说明并不需要使用4吨位的车,而且从全局考虑为了个别出车添加派车非常不符合实际情况,同时也不具有经济优势。
公里,说明并不需要使用4吨位的车,而且从全局考虑为了个别出车添加派车非常不符合实际情况,同时也不具有经济优势。
下载原稿pdf版本: 【Download】
作者保留所有后期权利,转载请注明出处.